応用情報｜木構造ってなに？５つの木の種類とその特徴を徹底解説！

木構造の基本知識

木（tree）とは、データの大小などをもとに、データを階層的に管理することに適したデータ構造です。

木構造を構成する要素には、様々な名前がついています。

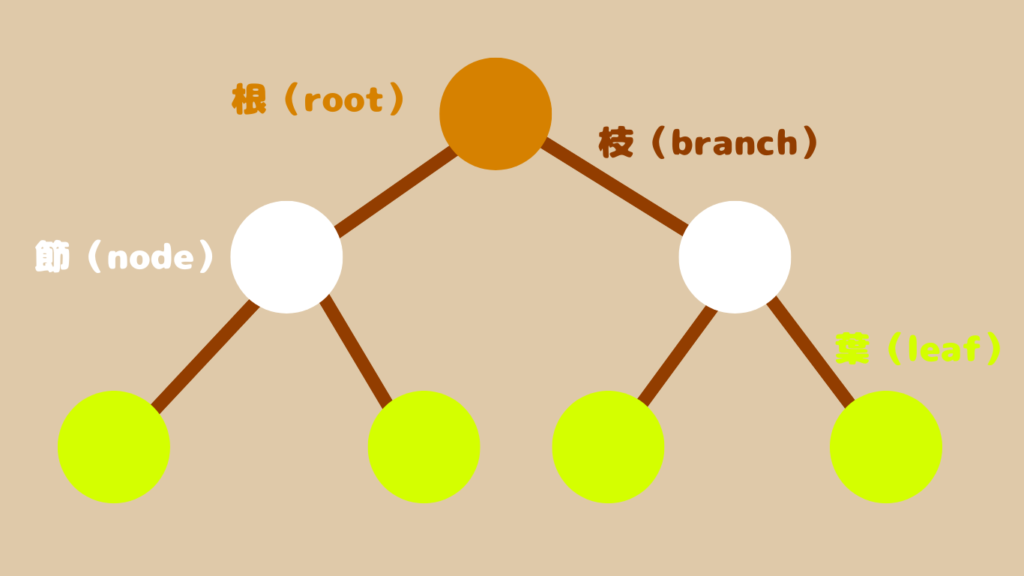
木構造の〇で示されるものは「節（node）」と呼ばれます。実際にデータを持っているのはこの部分で、木構造の肝となる部分です。

節同士をつなぐためにあるのが「枝（branch）」です。この枝で結ばれている節同士を、木構造では親子に例えて表します。枝を挟んで、上にある節を「親」、下にある節を「子」と呼びます。

節の中にも、特殊なものが２種類あります。いちばん上にある、親を持たない節が「根（root）」で、いちばん下にある、子を持たない節が「葉（leaf）」です。

木構造の縦の大きさを「深さ」と表現することもあり、主に根から葉までの最短の枝の数のことを指します。

これらの言葉は、午後問題の選択の１つであるアルゴリズムなどで、何の説明もなく問題文中に登場したりしますので、頭に入れておくことをおすすめします。

木構造の種類

ひとくちに木構造と言ってもたくさんの種類があります。紛らわしい名前もいくつかありますので、それぞれの特徴と名前を結び付けておきましょう。

木構造①　２分木

すべての節の子の数が２以下である木構造のことです。ほとんどの木はこのタイプです。

また、２分木と違い、すべての節の子の数が３以上である木を「多分木」と呼びます。

２分木は、木の探索方法がよく出題されます。「幅優先探索」と「深さ優先探索」の２種類があり、深さ優先順はさらに「先行順（行きがけ順）」「中間順（通りかけ順）」「後行順（帰りがけ順）」の３パターンに分けられます。

２分木の探索方法

幅優先探索は、根から近い節から順番に調べていく方法です。表を見るときと似たような感じで、節を一行ずつ、左から右に探索していきます。その名の通り、探索の際になるべく幅を確保するように、横に動くことが特徴です。

深さ優先探索は、根から葉に向かって、なるべく分岐せずに調べていく方法です。幅優先探索と逆に、なるべく深さを確保するように、縦に動くことが特徴です。

深さ優先探索の２パターンを識別するためによく用いられる方法は、根の左側からすべての節をなぞるようにぐるっと木を囲んだとき、線が節のどこを通るかを基準に順番を決める方法です。

具体的に、「先行順（行きがけ順）」は節の左側を線が通った順番に、節を並べます。「中間順（行きがけ順）」は節の下側を線が通った順番に、「後行順（帰りがけ順）」は節の右側を線が通った順番に並べます。

木構造②　完全２分木

２文木の中でも、葉以外のすべての節が２つの子を持ち、根から葉までの深さがどこを通っても等しい木のことを、「完全２分木」と呼びます。

葉の個数と深さを式で表すことができ、深さ「Ｈ」に対して、葉の数は「２のＨ乗」です。

木構造③　２分探索木

２分木の中でも、すべての節から見て、左側の子のデータが自分のデータよりも小さく、右側の子のデータが自分のデータよりも大きい木のことです。

つまり、分岐で左に行けば行くほどデータが小さくなっていき、分岐で右に行けば行くほどデータが大きくなっていきます。

２分探索木は、その名の通り２分探索に用いられる木です。探したい値と自分が持つ値を比べ、探したい値が小さければ左へ、大きければ右へ進んでいきます。

木構造④　バランス木

２分探索木の中でも、根から葉までの深さがほぼ一定になるように作られた木のことです。

２分探索木では、値の大小により右もしくは左に進んでいきます。そのため、左右のバランスがとれた木であれば、１度の分岐で要素の数を半分に絞ることができます。しかしバランスの良くない木であれば探索効率が悪くなりますよね。

バランス木は根から葉までの深さがほぼ一定、つまり要素の偏りがなく、バランスのとれた木です。そのため、探索効率が良い木と言えるでしょう。

バランス木には、「AVL木」と「B木」があります。

AVL木

２分木をベースにしたバランス木です。

左右の部分木の高さの差が１以下であることが特徴です。部分木とは、ある節とその節の子孫のことです。平たく言えば、ある節から葉までの範囲だと思って大丈夫です。

AVL木では、ある節から分岐している左の部分木、右の部分木で、その深さの差が１以下になります。

B木

多分木をベースにしたバランス木です。

外部記憶装置にデータを格納するための考えられた木構造で、様々な種類があります。データを格納するのは葉のみで、それ以外の節にはキーの値を持たせるだけという形も存在します。

木構造⑤　ヒープ木

２分木の中でも、親と子の間で必ず大小関係が決まっている木のことです。

「必ず親よりも子の値のほうが大きい」もしくは「必ず子よりも親の値のほうが大きい」という２つのパターンがあります。値の大小によって子の左右が決まらない（左右どちらでも関係ない）のが、２分探索木との違いです。

まとめ

今回は木構造についてまとめていきました。木構造は、ソートのアルゴリズムでよく用いられます。長い問題文、複雑なプログラム、たくさんの変数で頭がパンクしてしまいそうな状態で、よく理解できていない木構造の問題は解きづらいですよね。木構造の仕組みを理解しておけば、問題を解くカギになるかもしれません。

次のステップへ：応用情報技術者試験合格者の声

合格者の体験​​談と学習のコツ